8.3 Reinforcement learning
Reinforcement learning (RL) is the most complex concept of the learning classes. It helps to first look at a simple example where the goal is to find the best possible way in a grid world. How the best possible way is defined and ways to find it will be the topic of this chapter
8.3.1 Elements of reinforcement learning
There are five elements of RL as depicted below:
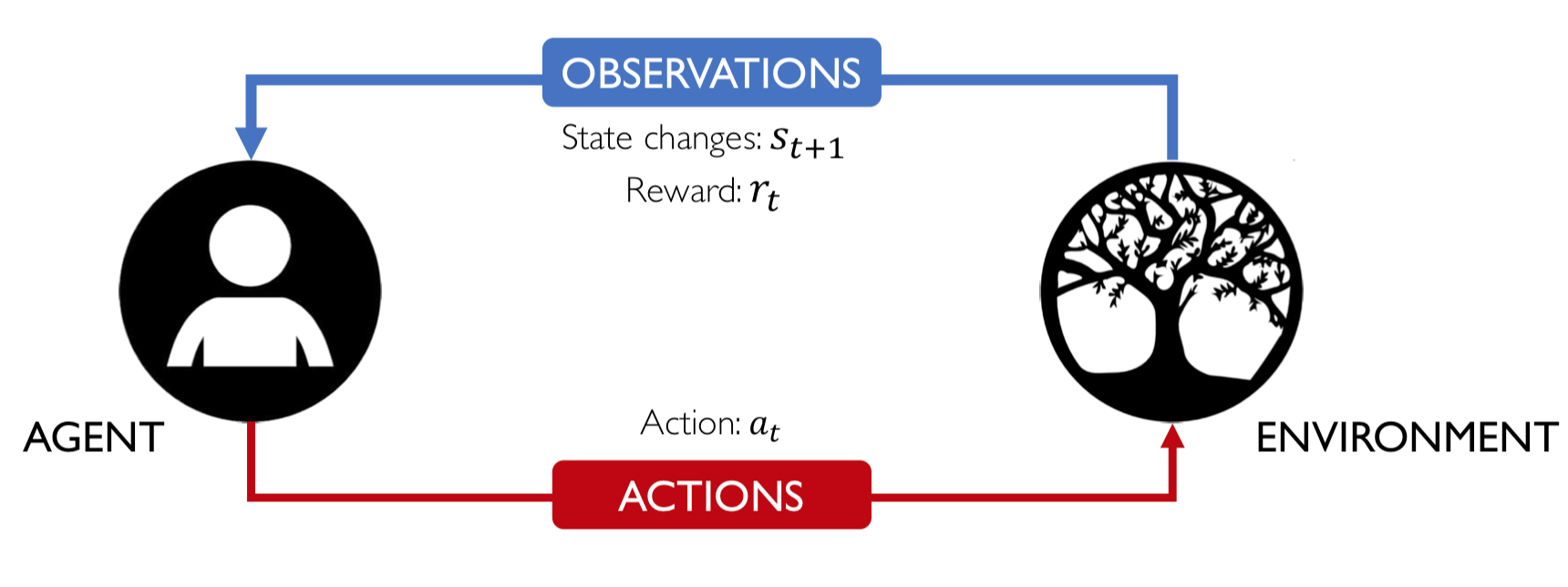
Figure from © MIT 6.S191: Introduction to Deep Learning
Those elements together build a Markov decision process (MDP) which might be a more familiar term. In order to solve a taks using RL the first step would be if the real world problem can be described as a MDP in terms of the five RL elements.
Elements of RL:
- Agent: takes actions.
- Environment: the world in which the agent exists and operates.
- Action \(a_t\): a move the agent can make in the environment.
- Observations: of the environment after taking actions.
- State \(s_t\): a situation which the agent perceives.
- Reward \(r_t\): feedback that measures the success or failure of the agent’s action.
- State \(s_t\): a situation which the agent perceives.
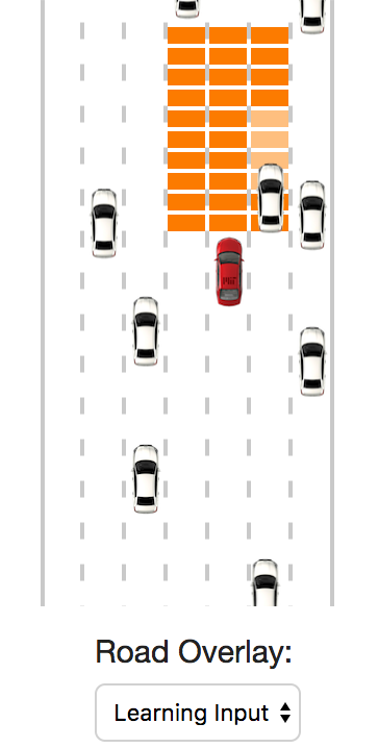
In order to understand the above defined terms better it is helpful to look at an example of self driving car in a simulator of MIT (https://selfdrivingcars.mit.edu/deeptraffic/).
The agent is the car which can take any of five actions
Actions of agent \(a_t\):
- No action
- Accelerate
- Break
- Change lanes
- to the left
- to the right
The environment is the red marked space segments of the road The state is defined by the spaces in environment which are occupied by another car or empty. The reward is given by the speed of the car, the faster the better
A close look at the reward shows that the reward is summed up over time weighted with the so called discount factor \(\lambda\) which is in the range of \(0\geq \lambda \leq 1\). Therefore the reward is not only dependent on the immidient reward but also on the to be expected reward.
\[R_{t}=\sum_{i=t}^{\infty} \gamma^{i} r_{i}=\gamma^{t} r_{t}+\gamma^{t+1} r_{t+1} \ldots+\gamma^{t+n} r_{t+n}+\dots\]
A Q-function can be defined which gives the expected value of the total reward for an action \(a\) in a given state \(s\).
\[Q(s, a)=\mathbb{E}\left[R_{t}\right]\]
where \(\mathbb{E}\) is the expected value of the total reward. So the equation can be read as:
Q value if the environment is in state \(s\) and the agent performing action \(a\) is the expected value of the total reward \(\mathbb{E}\left[R_{t}\right]\)
The Q-function captures the expected total future reward an agent in state \(s\) can receive by executing a certain action \(a\) .
Ultimately, the agent needs a policy \(\pi(s)\), to infer the best action to take at its state \(s\)
The strategy is that the policy should choose an action that maximizes future reward
\[\pi^{*}(s)=\underset{a}{\operatorname{argmax}} Q(s, a)\]
8.3.2 RL algorithms
There are two ways to learn the best action
Value learning
Policy learning

Figure from © MIT 6.S191: Introduction to Deep Learning
8.3.2.1 Value learning
The task in value learning is to find the Q-values for the states and acitons \((s,a)\)
Depending on the complexity of the environment it might be difficult to find the Q values.
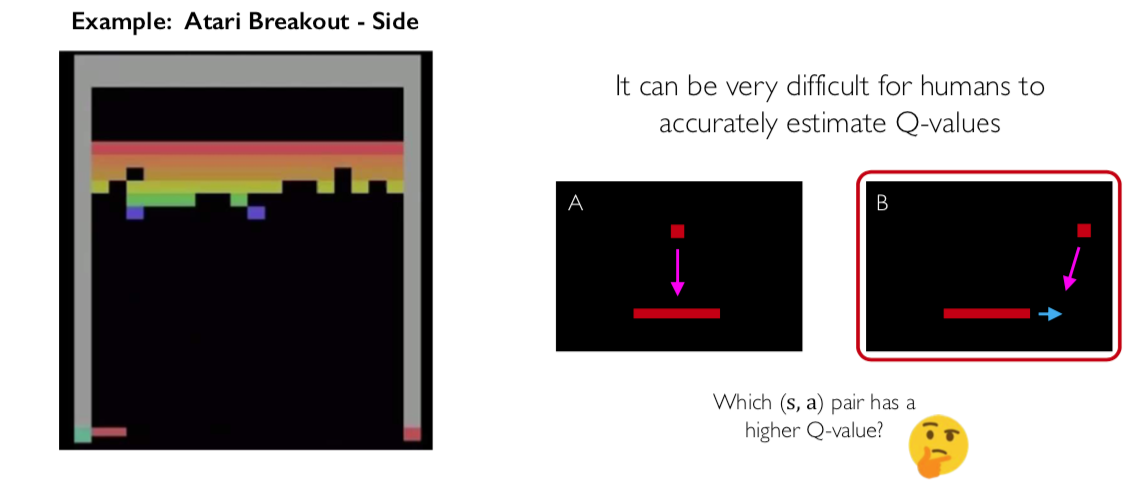
Figure from © MIT 6.S191: Introduction to Deep Learning
Q-values can be found using neural networks, the training however is than a two staged task.
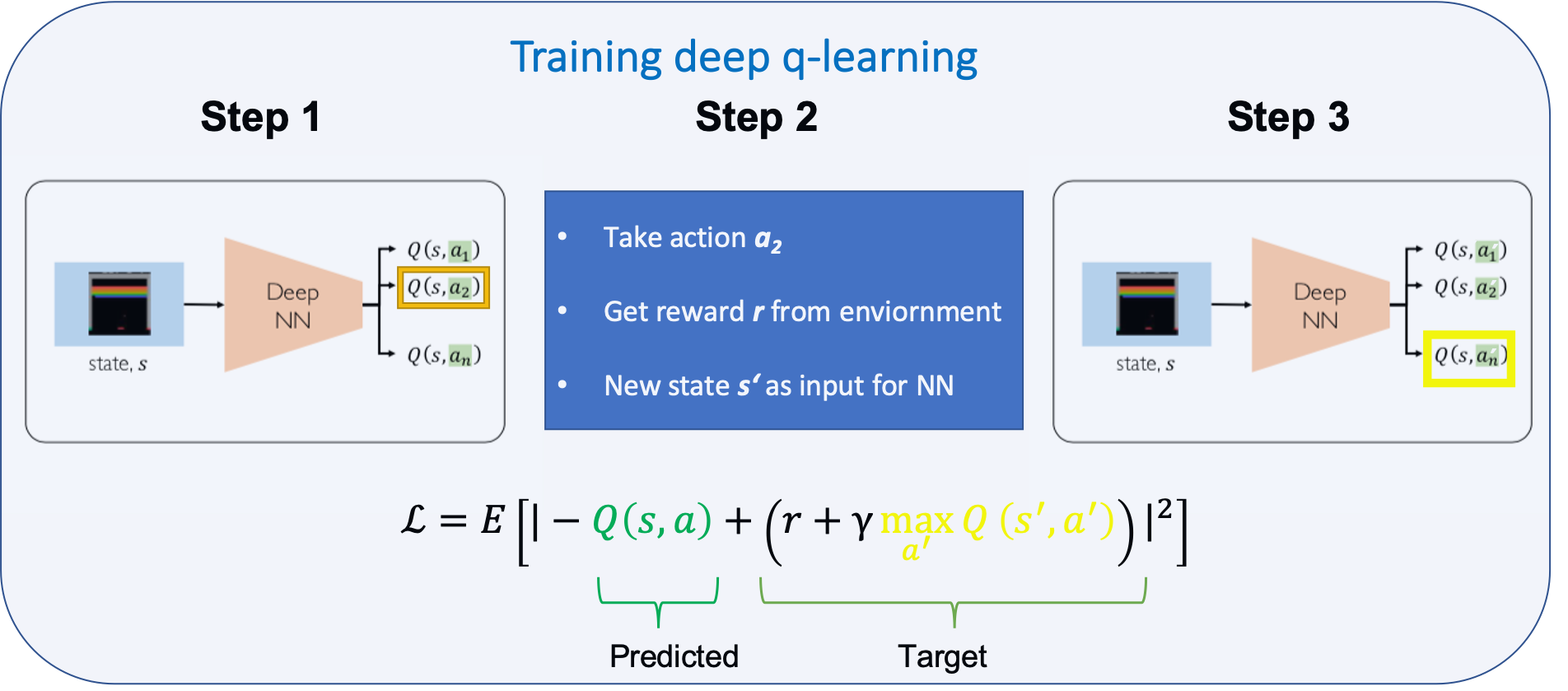
Figure based on © MIT 6.S191: Introduction to Deep Learning
Q-learning downsides:
- Complexity:
- Can model scenarios where the action space is discrete and small
- Cannot handle continuous action spaces
- Flexibility:
- Cannot learn stochastic policies since policy is deterministically computed from the Q function
8.3.2.2 Policy learning
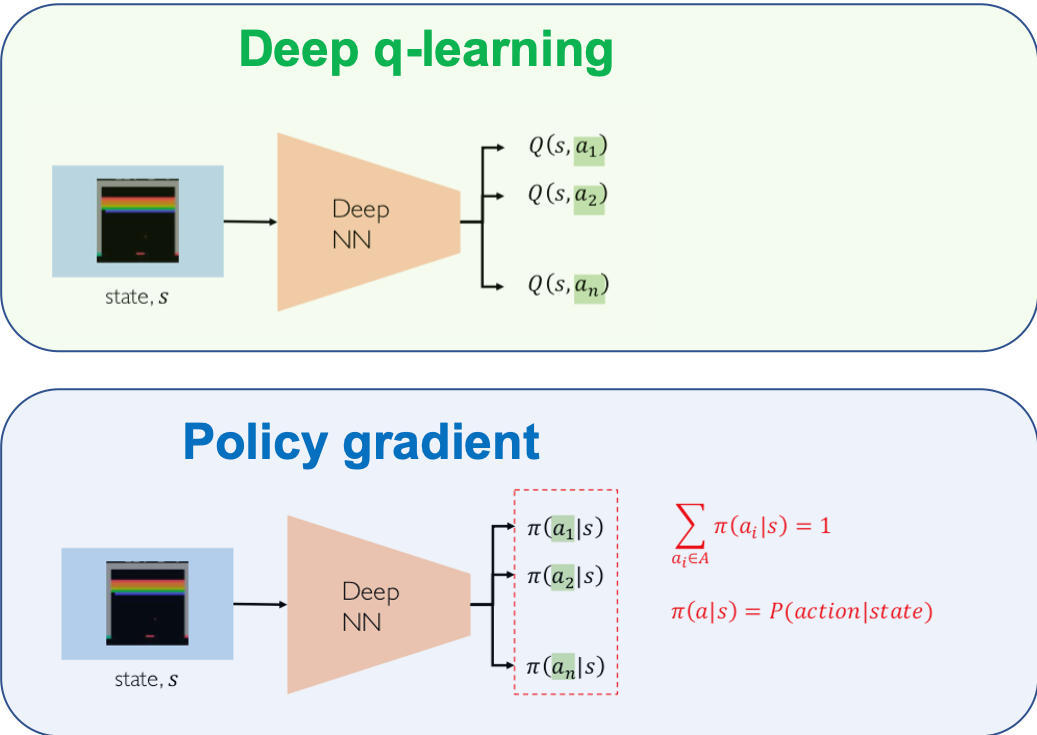
Figure based on © MIT 6.S191: Introduction to Deep Learning
- Run a policy for a while
- Increase probability of actions that lead to high rewards
- Decrease probability of actions that lead to low/no rewards
In a more mathematically way this could be written as pseudo code
Pseudo code for training:
- function REINFORCE
- Initialize \(\theta\)
- \(\mbox{for episode} \sim \pi_{\theta}\)
- \(\left\{s_{i}, a_{i}, r_{i}\right\}_{i=1}^{T-1} \leftarrow episode\)
- for t = 1 to T-1
- \(\nabla \leftarrow \nabla_{\theta} \log \pi_{\theta}\left(a_{t} | s_{t}\right) R_{t}\)
- \(\theta \leftarrow \theta+\alpha \nabla\)
- return \(\theta\)
where \(\log \pi_{\theta}\left(a_{t} | s_{t}\right)\) is the log-likelihood of action \(a_t\)
8.3.3 Example self driving car MIT
The DeepTraffic website of MIT is a great place to get a feeling for reinforcement learning. Parameters can be varied and the impact can be seen right away without the need to install any code on the computer.
DeepTraffic: - Competition of MIT in the frame of their self-driving car course - Target: Create a neural network which drives a car fast through highway traffic - website https://selfdrivingcars.mit.edu/deeptraffic/ - documentation: https://selfdrivingcars.mit.edu/deeptraffic-documentation/
The following variables control the size of the input the net gets – a larger input area provides more information about the traffic situation, but it also makes it harder to learn the relevant parts, and may require longer learning times.
Environment:
For each car the grid cells below it are filled with the car’s speed, empty cells are filled with a high value to symbolize the potential for speed.
Your car gets a car-centric cutout of that map to use as an input to the neural network. You can have a look at it by changing the Road Overlay to Learning Input
lanesSide = 1;
patchesAhead = 10;
patchesBehind = 0;
The agent is controlled by a function called learn that receives the current state (provided as a flattened array of the defined learning input cutout), a reward for the last step (in this case the average speed in mph) and has to return one of the following actions:
Ouptut of neural network is action:
- Agent is controlled by function called learn
- Receives current state
- flattened array
- reward of last step
retunrs
>
var noAction = 0;
var accelerateAction = 1;
var decelerateAction = 2;
var goLeftAction = 3;
var goRightAction = 4;
The learn function is as follows
learn = function (state, lastReward) {
brain.backward(lastReward);
var action = brain.forward(state);
draw_net();
draw_stats();
return action;
}An overview of the most important variables is given below

8.3.3.1 Crowdsourced Hyperparmeter tuning
MIT “DeepTraffic: Crowdsourced Hyperparameter Tuning of Deep Reinforcement Learning Systems for Multi-Agent Dense Traffic Navigation” (Fridman, Terwilliger, and Jenik 2018) in which they present the results of
Results of study:
- Number of submissions: 24,013
- Total network parameters optimized: 572.2 million
- Total duration of RL simulations: 96.6 years
The results show that over time the results became better until a plateau was reached.
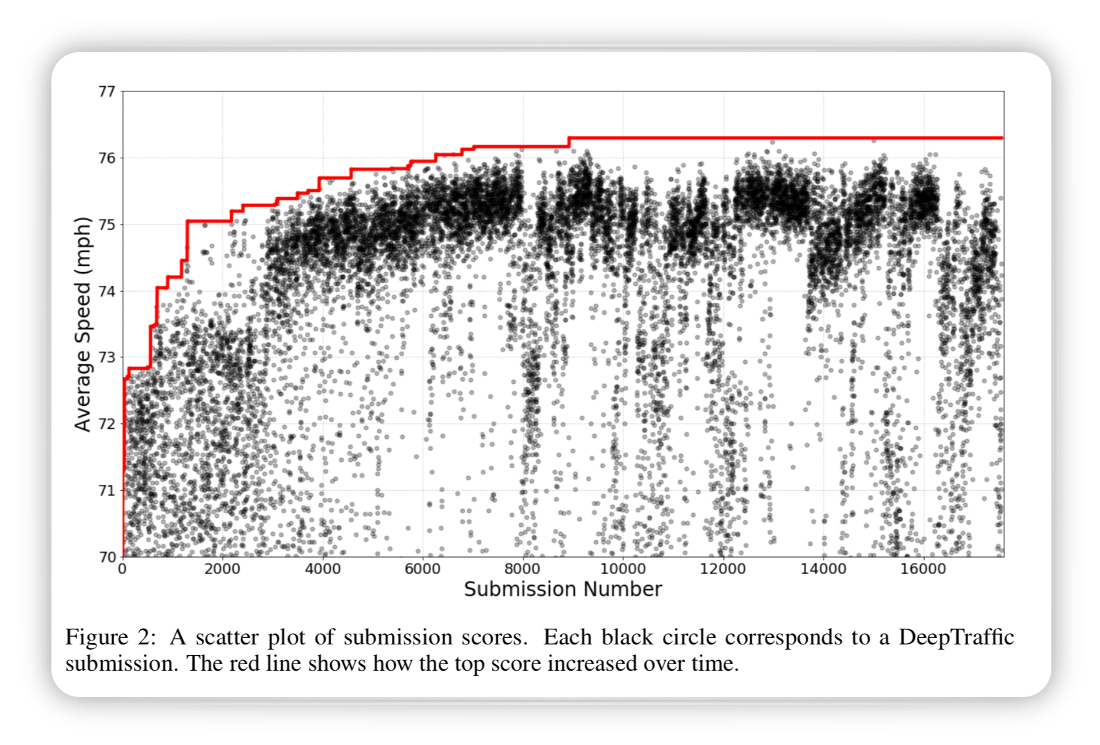
Figure from (Fridman, Terwilliger, and Jenik 2018)
Looking at average speed vs neural network parameters it can be seen that
Average speed vs NN parameters:
- Few layers sufficient for high average speed
- Balance needed between neural network
- width
- deepth
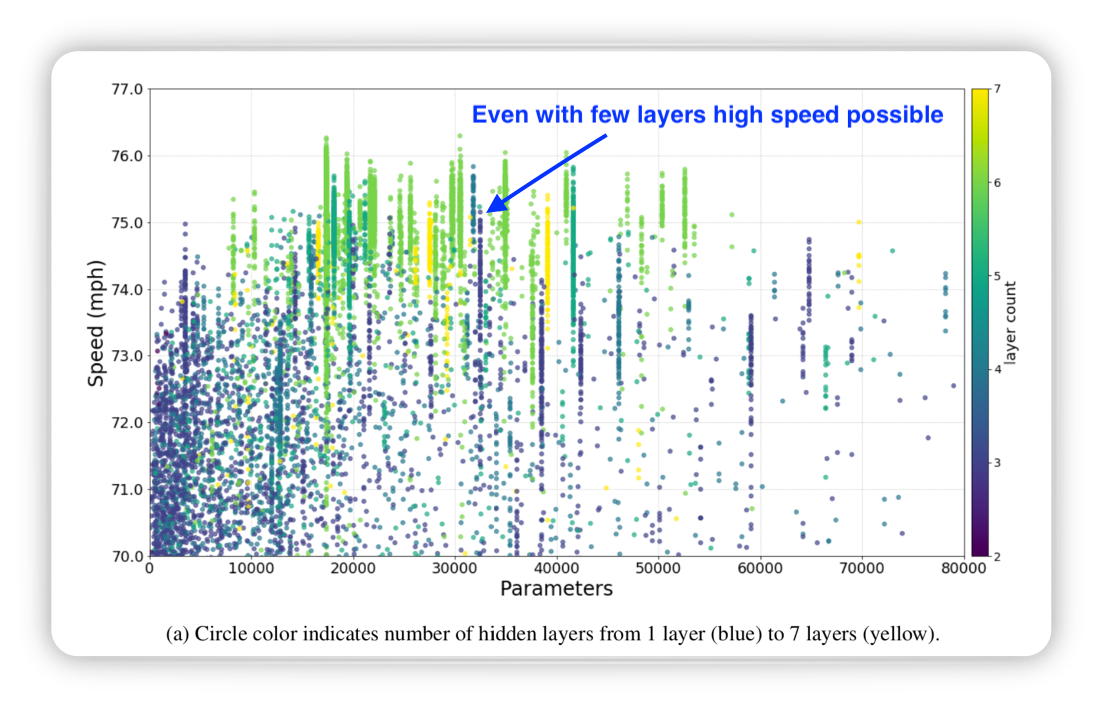
Figure from (Fridman, Terwilliger, and Jenik 2018)
Looking at the training iterations it can be seen that with fewer parameters less iterations are necessary
Figure from (Fridman, Terwilliger, and Jenik 2018)
There is a clear optimum of three lines at either side of the car
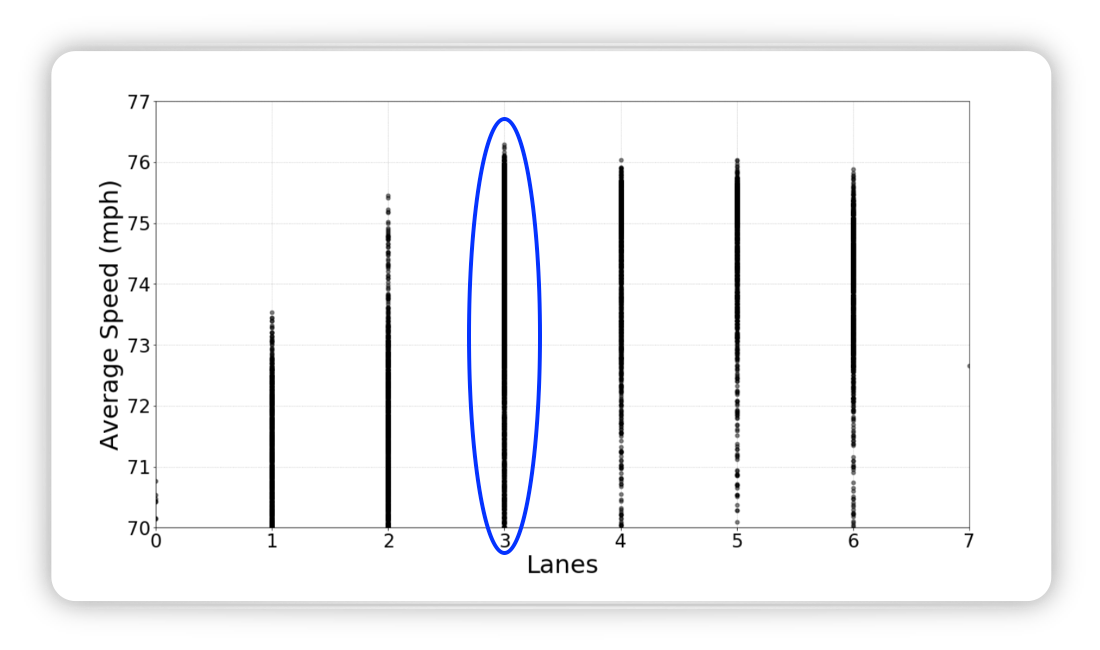
Figure from (Fridman, Terwilliger, and Jenik 2018)
It can be concluded that it is worth looking into the future when looking at the image below depicting average speed vs pachtes ahead.
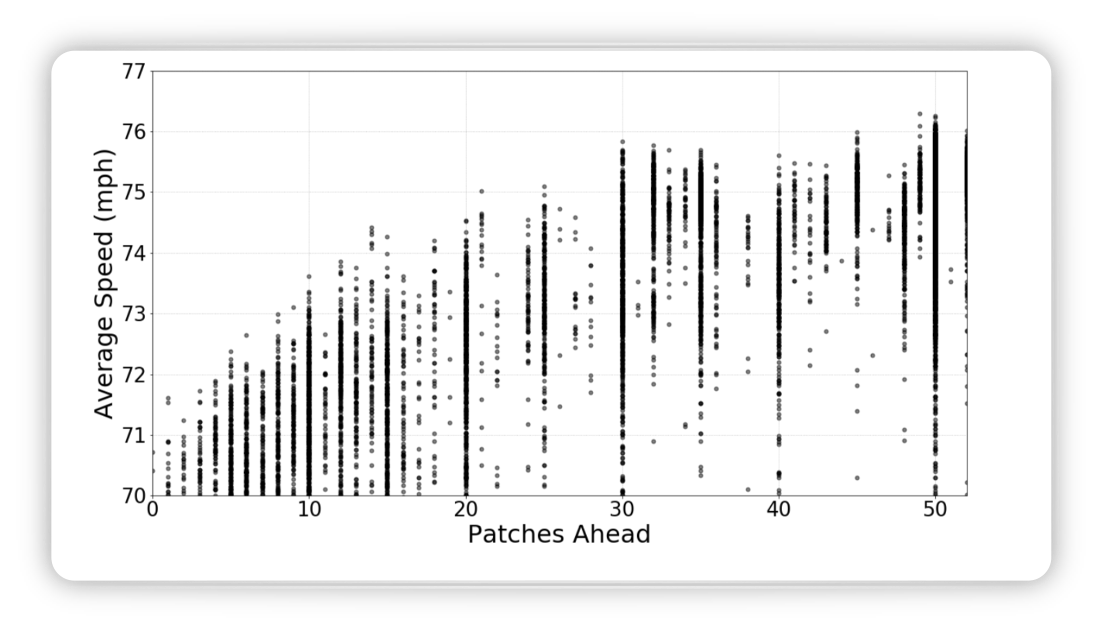
Figure from (Fridman, Terwilliger, and Jenik 2018)
Whereas looking into the past only pays of until 5 patches behind.
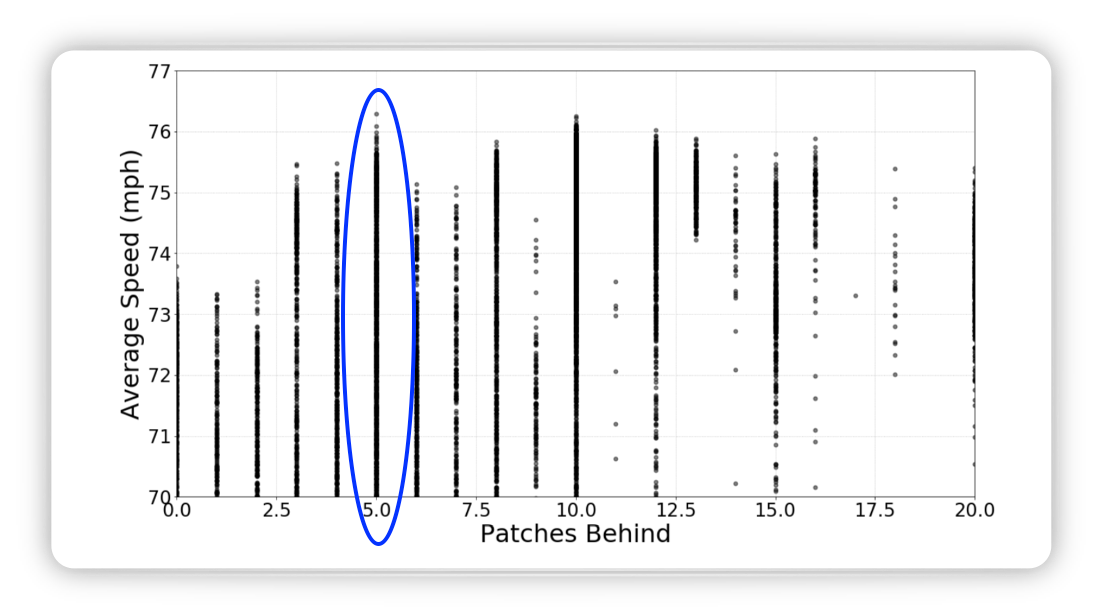
Figure from (Fridman, Terwilliger, and Jenik 2018)
Another idea to improve the performance is to look not only at one image but at several images to get a bette understanding of the dynamics of the scenario. However, the graph below shows that is was not helpful to look into the past
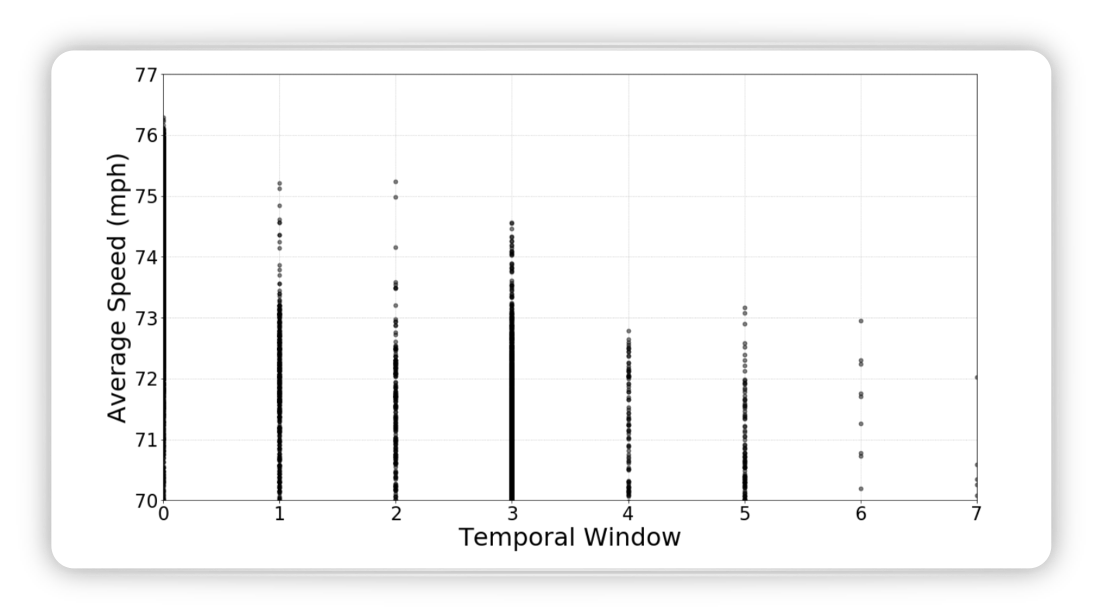
Figure from (Fridman, Terwilliger, and Jenik 2018)
The reduction factor \(\gamma\) considers future rewards, the higher the value the more attention is given to future awards. The image below shows that paying attention to future rewards is beneficial
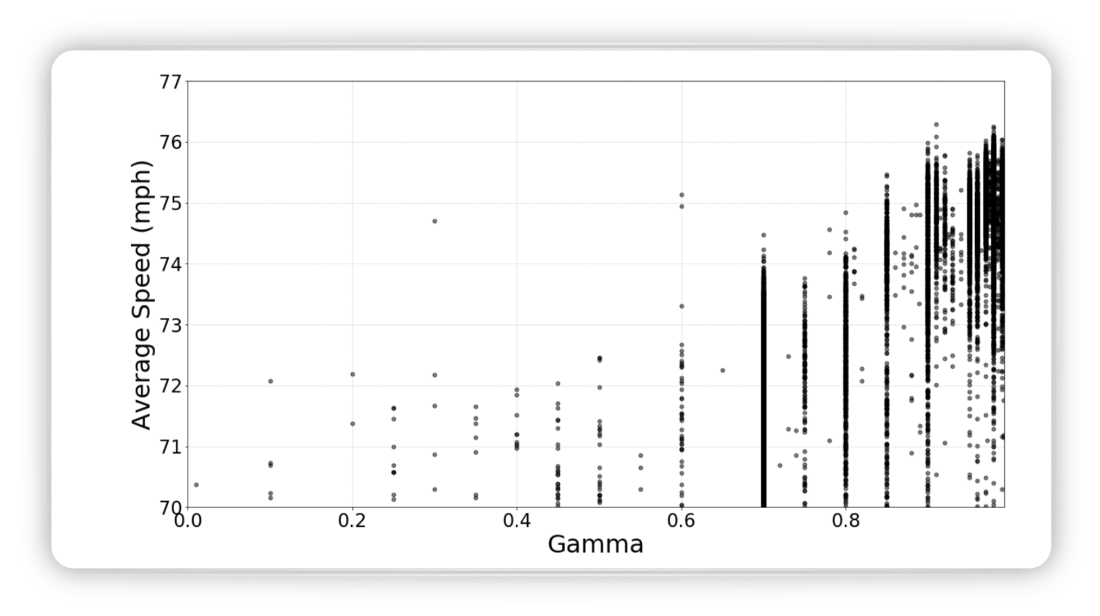
Figure from (Fridman, Terwilliger, and Jenik 2018)
To find a rule out of the parameters analysed a t-SNE mapping of the following parameters onto 2 dimensions was conducted:
- patches ahead
- patches behind
- l2 decay
- layer count
- gamma
- learning rate
- lanes side
- training iterations
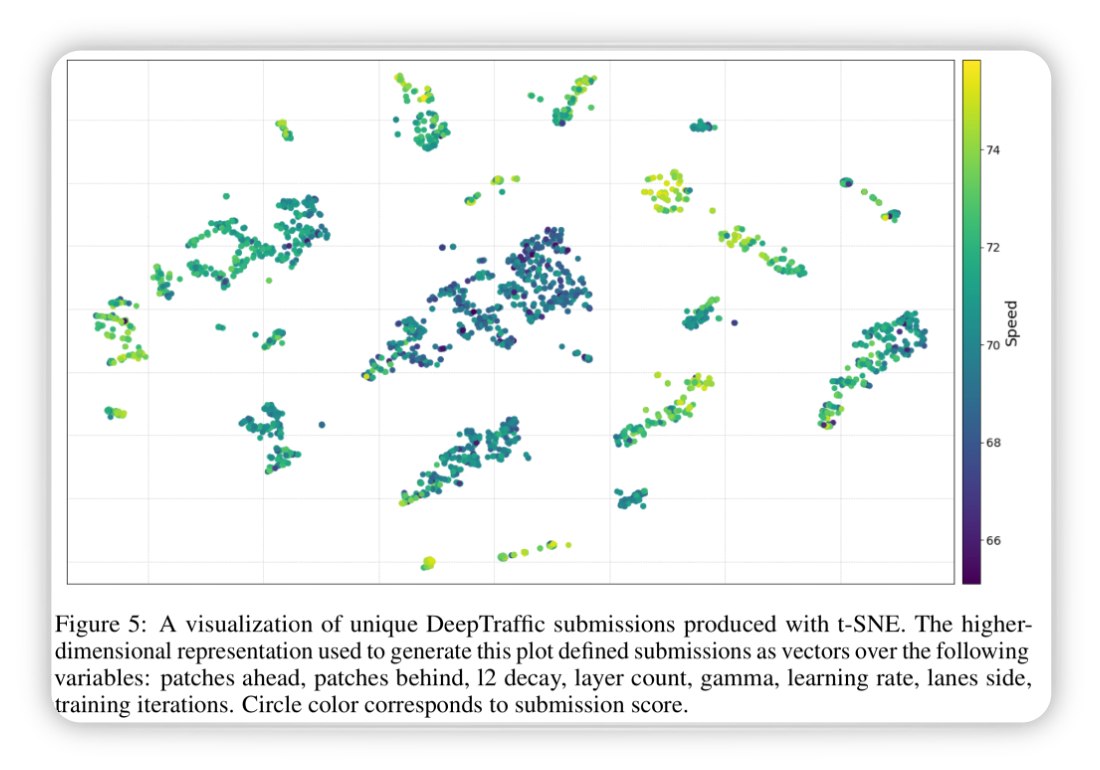
Figure from (Fridman, Terwilliger, and Jenik 2018)
The figure shows spots with high average speed, those patches can be used as basis for further improvement.