9.1 Linear regression
A linear regression is a regression analysis, a statistical method, at which a dependent variable is explained through several independent variables.
- Simple linear regression
- Only one independent variable
- Multiple linear regression
- more than one independent variables
Linear regression algorithm is one of the fundamental supervised learning algorithms.
9.1.1 Example for linear regression
In this example the procedure of a linear regression is described
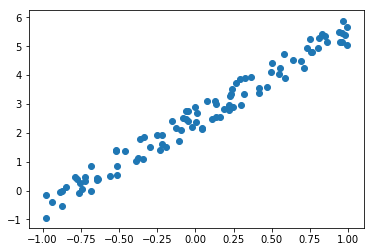
Data
Given is a set of data created by a linear expression plus some noise
\[y = 3*x+2+n\] where \(n\) is noise
The data can be depicted as below. It is easy to be seen that we are looking at a linear function with superimposed noise.
Model
The task is to find the value for \(w_0\) and \(w_1\) of a model which is as close as possible to the original function
\[\hat{y} = w_0*x+w_1\]
Loss function
The metric to define how good the model fits the data is defined as mean squared error (MSE)
\[L=(\hat{y}-y)^2\]
Minimise loss function
The difference between \(\hat{y}\) and \(y\) shall be small stochastic gradient descent (SGD) can be applied.
SGD:
- Iteratively updating values of \(w_0, w_1\) using
- gradient
- learning rate \(\eta\)
In maths terms this can be written as:
A graphical representation of SGD is given below. In this example the loss function can be depicted as a 3D plot. In the current case the surface is flat which makes it easy to find the global optimum
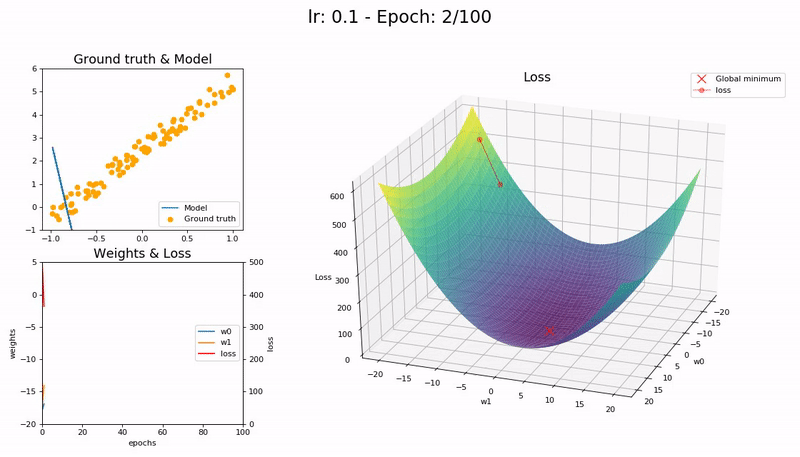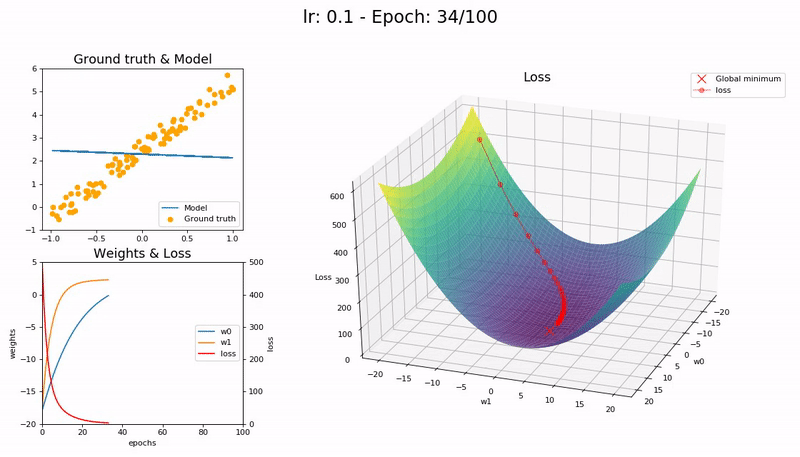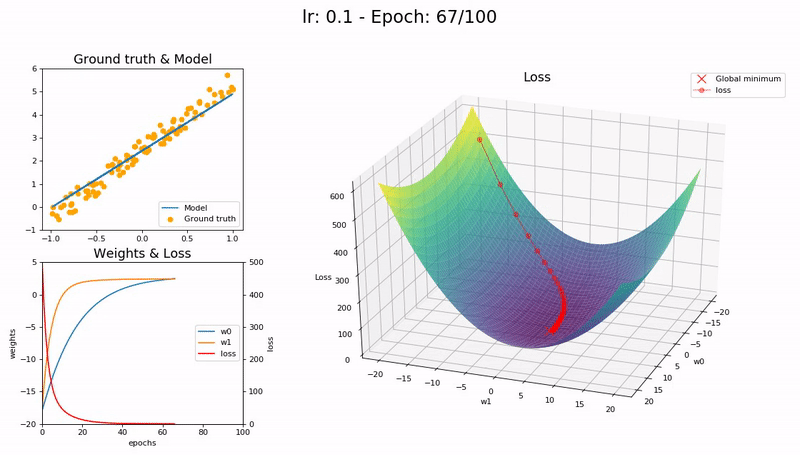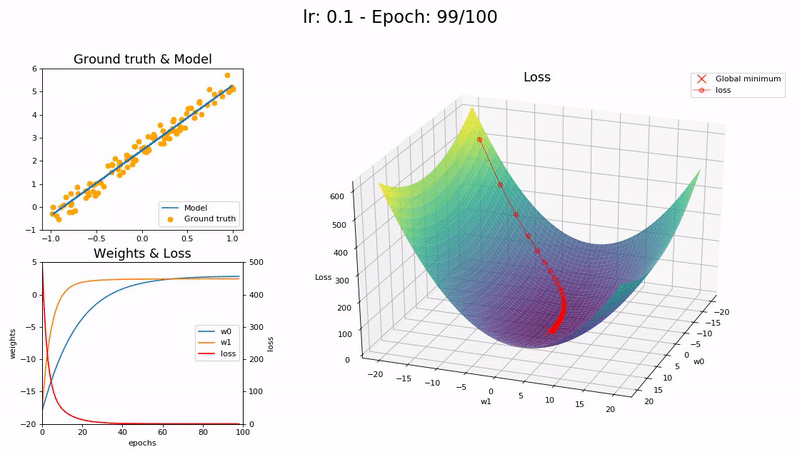
Figure from https://nbviewer.jupyter.org/gist/joshfp/85d96f07aaa5f4d2c9eb47956ccdcc88/lesson2-sgd-in-action.ipynb