3.6 Solution of the Schrödinger equation using deep neural networks
In this chapter two different approaches to solve the Schrödinger equation are compared both exploiting the fact that neural networks are universal function approximators. A group with members of FU Berlin, TU Berlin and Rice University describe in their paper “Deep-neural-network solution of the electronic Schrödinger equation” (Hermann, Schätzle, and Noé 2020) an approach where they combine the neural network with fixed functions. They state:
The electronic Schrödinger equation describes fundamental properties of molecules and materials, but can only be solved analytically for the hydrogen atom.
Their model is shown below
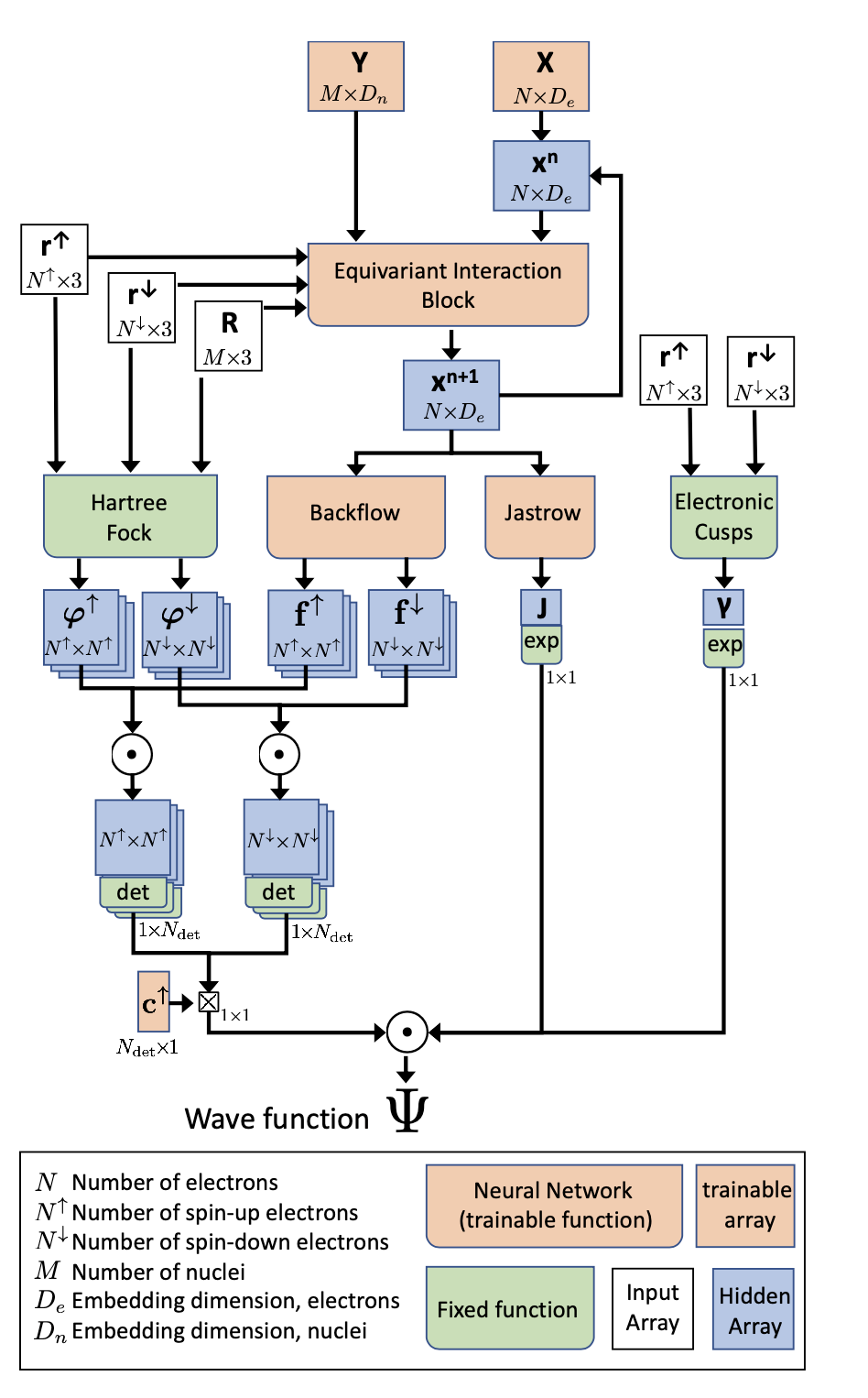
Information flow in the PauliNet ansatz architecture, Figure from (Hermann, Schätzle, and Noé 2020)
The advantage of mixing neural networks and fixed functions is that known principles do not have to be learned by the network. Comparing their approach with the DeepMind approach they conclude:
The residual error of FermiNet is even smaller than that of PauliNet, but at the expense of computational cost that is approximately two orders of magnitude greater. …
However, the results reported by (Pfau et al. 2020) were obtained with about 30 times more electronic samples for training, using eight state-of-the-art graphics processing units in parallel instead of one in our case.
A group with members of Deepmind and Imperial college describe in their paper “Ab initio solution of the many-electron Schrödinger equation with deep neural networks” (Pfau et al. 2020) an approach where they use only a neural network.
Their model is shown below
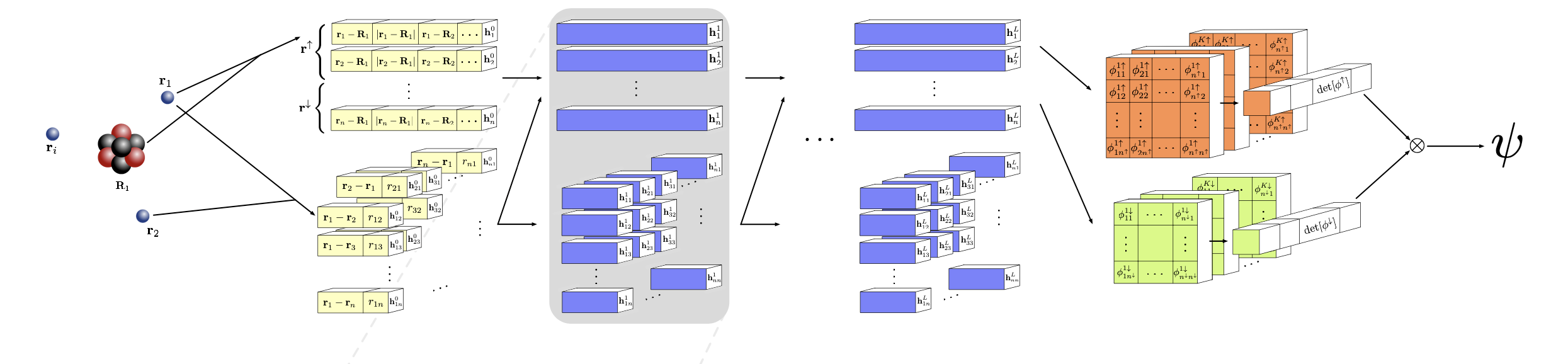
The Fermionic Neural Network (Fermi Net), Figure from (Pfau et al. 2020)
Comparing the two approaches
- Reduce computational cost by introducing fixed functions into the model
- Impact on training
- Derivative of fixed funciton has to be known?
- Is that covered by using PyTorch?
- Impact on training
- Probably less domain knowledge necessary to built pure neural network solution